12b - ODE Example

CO2 concentration in a Terrarium from balance equations

Derivative of CO2 with respect to time:

\[ \frac{dCO2}{dt} = D\cdot(C^{out}_{CO2} - CO2) + V_{soil}b - dLA\cdot C_{CO2} \]

#import packages
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# set constants
D = 1
CCO2out = 400 #outside ppm of CO2
Vsoil = 0.03 #volume of soil
b = 20 #rate of CO2 production from the soil
d = 0.1 #rate of photosythesis
L = 100 #lux level of light
A = 0.2 #surface area of plant mater photosythesisizing

#define your derivative
def derivative(CO2, time):
    diff = D*(CCO2out - CO2)
    gen = Vsoil*b
    cons = d*CO2*L*A
    return diff + gen - cons

derivative(40000,0)

-119599.4

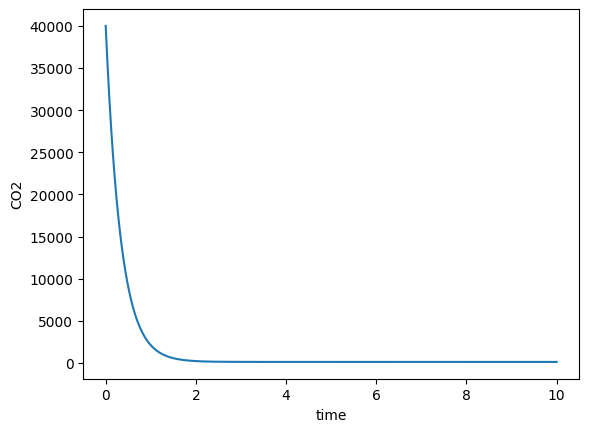
time = np.linspace(0,10,1000)

sol = odeint(derivative,40000,time)

plt.plot(time,sol)
plt.xlabel('time'); plt.ylabel('CO2')

Text(0, 0.5, 'CO2')