17-Mole Balances#
Mass (mole) and energy balance problems are fundamental to chemical engineering. It takes practice to understand how to set up and solve these problems. These problems are part of multiple courses in chemical engineering, and they are also part of the Fundamentals of Engineering (FE) exam and proficiency exams given by chemical engineering departments. This course is the 2nd or 3rd time reviewing theses principles. Example exam results demonstrating that more practice is needed are shown below.

Mass and Energy Balances#
Helpful sheet: General Mass and Balance Equations
Why?: Concentration Estimates for Assessing Risk#
Prior to implementing control techniques, it can be important to quantify the risk of exposure from a spill scenario of other toxic gas/ vapor release.
Total Mole (Mass) and Component Mole Balances#
Given a control volume and:
A release of toxic gas or vapor at a constant rate
Addition of air at a constant rate
Exit of the gasses based on the inlet conditions and assuming that the exit rate can be achieved without pressurization of the control volume
Steady state conditions
Total molar balance:
Component balances:
At steady state, the accumulation terms (\( \frac{dn_{tot}}{dt} \) and \( \frac{dn_{i}}{dt} \)) are zero.
Other assumptions/ notation:
concentration of interest, \( C_i = n_i/V \),
the exit rate of the total gases is \( Q^n_v \), mol//time,
the inlet rate of the composition of interest is \( Q^e \), mol//time,
\( C_{ppm} = C_iRT/P\cdot 10^6 \), where \( C_{ppm} \) is the concentration in parts per million (ppm), \( R \) is the ideal gas constant, \( T \) is the temperature, and \( P \) is the pressure.
\( n_{gen,i} = 0 \), for the case of a spill or release of a toxic gas or vapor (new species are not generated).
Perfect mixing of the gases in the control volume (no concentration gradients).
As such, the mole balance for the component of interest i is
If however, there are concentration gradients, the concentration could deviate significantly from the above estimate (larger or smaller).
Inlet composition from vaporization of a liquid#
The inlet rate of the species of interest, \( Q^e \), can be estimated from the vapor pressure of the liquid and the rate of vaporization and a mass transfer coefficient according to:
where \( k_m \) is the mass transfer coefficient, \( C_{sat} \) is the saturation concentration of the species close to the liquid surface, and C is the concentration of the species in the air, and \( A \) is the area of the spill.
\( k_m \) can be estimated from correlations or from experimental data or by comparison to another component with a known mass transfer coefficient (e.g. water, \( k_m^0 \)).:
where \( M \) is the molecular weight of the species of interest and \( M_0 \) is the molecular weight of water. \( k_m^0 \) is typically in the range of \( 0.1-10.0 \, \text{cm/s} \) depending on the conditions.
\(C_{sat}\) can be estimated from the Antoine equation:
where \( P_{sat} \) is the saturation pressure of the species of interest, and \( A \), \( B \), and \( C \) are constants that can be found in the literature. Where \( C_{sat} \) = \( P_{sat}/RT \).
Incorporating those into the mole balance, we have:
How would you solve the above if you would like the unsteady state concentration as a function of time? And there by obtain the Time Weighted Average (TWA) for a worker directly after a spill?
See here to view a video on a mole (mass) balance for a spill scenario. This video can be helpful for the homework. You can download the sheet used in the video here: clint-bg/safetyinjc
Additional Mass Balance Examples#






Mass and Energy Balance Example#



#Mass and energy balance solution for Example 4
# air flow into room at 20C, methane flow into room at 200C, air/methane mixture leaves the room
# determine the fraction of methane and air temperature as a function of time
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Parameters
Cv_m = 27 # J/mol-K specific heat of methane, (estimate) assumed constant but is a function of temperature
Cv_air = 29 # J/mol-K specific heat of air, (estimated) assumed constant but is a function of temperature
#stream flow rates
nin_air = 1 # mol/s air flow rate
nin_m = 1/7 # mol/s methane flow rate
#stream temperatures
Pairin = 101425 # Pa, pressure of air stream entering the room
Tairin = 20 + 273.15 # K, temperature of air entering the room
Tmin = 200 + 273.15 # K, temperature of methane entering the room
#room parameters
orifice_diameter = 0.2 # m (outlet diameter)
Cd = 0.6 # discharge coefficient
Pext = 101325 # Pa, external pressure
P_initial = Pext # Pa, constant pressure
T_initial = 20 + 273.15 # K, initial temperature of room
n_initial = 1000 # total moles in room, can be found from the volume and initial temperature and pressure
nm_initial = 0 # initial moles of methane in room
Rg = 8.314 # J/mol-K
T0 = 20 + 273.15 # K, reference temperature
Pref = 101325 # Pa, constant pressure
Vol = n_initial * Rg* T_initial/P_initial # m^3, volume of room
print(f'Volume of room = {Vol} m^3')
print(f'Air flow rate into room = {nin_air*Rg*Tairin/Pairin} m3/s')
print(f'Air flow rate into room = {nin_air} mol/s')
def derivatives(p,t):
# changing parameters
n, nm, T = p
ym = nm/n
Cv = ym * Cv_m + (1-ym) * Cv_air # J/mol-K, specific heat of the mixture
Mw = ym * 0.016 + (1-ym) * 0.029 # kg/mol, molecular weight of the mixture
P = n*Rg*T/Vol # Pa, pressure in the room
rho = P*Mw/Rg/T # kg/m^3, density of the mixture
# flow rate out, assume flow out is incompressible
nout = Cd * np.pi/4 * orifice_diameter**2 * np.sqrt(2*(P-Pext)*rho)/Mw # mol/s
# Mass balance
# first total mass balance
dndt = nin_air + nin_m - nout
# then component balance
dnmdt = nin_m - nout * ym
# Energy balance
dTdt = 1/(n*Cv)*(- Cv*(T-T0)*dndt + nin_air*(Cv_air+Rg)*(Tairin-T0) + nin_m*(Cv_m+Rg)*(Tmin-T0) - nout*(Cv+Rg)*(T-T0))
return [dndt, dnmdt, dTdt]
# time points
t = np.linspace(0,1000,1000) # seconds
# solve ODE
n0 = [n_initial, nm_initial, T_initial]
sol = odeint(derivatives, n0, t)
# plot results in a grid of subplots
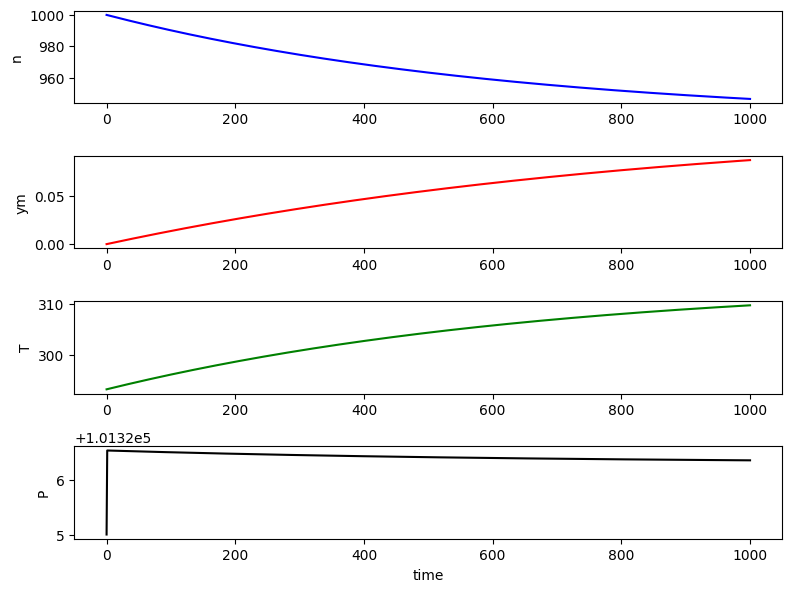
fig, ax = plt.subplots(4, 1, figsize=(8, 6))
ax[0].plot(t, sol[:, 0], 'b', label='n')
ax[0].set_ylabel('n')
ax[1].plot(t, sol[:, 1]/sol[:,0], 'r', label='ym')
ax[1].set_ylabel('ym')
ax[2].plot(t, sol[:, 2], 'g', label='T')
ax[2].set_ylabel('T')
ax[3].plot(t, sol[:, 0]*Rg*sol[:,2]/Vol, 'k', label='P')
ax[3].set_ylabel('P')
ax[3].set_xlabel('time')
fig.tight_layout(pad = 1.0)
plt.show()
Volume of room = 24.053778435726617 m^3
Air flow rate into room = 0.024030062607838305 m3/s
Air flow rate into room = 1 mol/s
Control Techniques#
There are multiple control techniques that can be used to reduce the exposure to workers from a toxic gas or vapor. These include:
Inherent Safety: Designing the process to eliminate or reduce the use of toxic gases or vapors.
Substitution: Replace the toxic gas or vapor with a less toxic or non-toxic alternative.
Minimization: Reduce the amount of toxic gas or vapor that is used in the workplace.
Isolation: Use of barriers or other methods to separate the toxic gas or vapor from workers.
Engineering Controls: Use of ventilation, enclosures, or other engineering controls to reduce the concentration of the toxic gas or vapor in the workplace.
Administrative Controls: Use of work practices, policies, and procedures to reduce the exposure of workers to toxic gases or vapors.
Personal Protective Equipment (PPE): Use of PPE such as respirators (full or half face) or supplied air respirators to reduce the exposure of workers to toxic gases or vapors.
Engineering Controls#
Ventilation: Ventilation occurs with HVAC systems where air is circulated and filtered. However, most of the air is recirculated and only a small fraction is replaced with fresh air. The recirculation of air can lead to a build up of toxic gases and or distribute them to other areas of the workplace.
Ventilation where outside air is brought in can help reduce the concentration of toxic gases or vapors but it has significant energy costs.
Typical ventilation occurs with negative rather than positive pressure systems. Know the difference between positive and negative pressure systems and why one might be used over the other.
Local Venilation: Hoods
Hoods are effective at containing an expelling toxic gases or vapors. However, they can be expensive to install and maintain. They also require a significant amount of energy to operate.

